¿Por qué, después de solo 10 días en mi nuevo ciclo de facturación, recibiría una alerta de que se ha utilizado el 90% de mi plan mensual de internet de 125 GB y todavía me quedan 20 días? Sé que el uso promedio de mi hogar en los últimos ocho meses ha sido de 70-80 GB. También sé que mi hija trabajó en la ciudad durante el verano, pero regresó a casa para las vacaciones de diciembre (llegó el 21 de diciembre).
Después de acceder a los datos de la compañía telefónica y descargar los datos de uso de los últimos dos meses, veo una oportunidad para algunas «estadísticas básicas» que luego puedo compartir con mi hija a medida que nos acercamos al tema del abuso desenfrenado de transmisión por internet… Nos llevaremos estos datos a Minitab y generaremos algunas estadísticas descriptivas y un histograma.
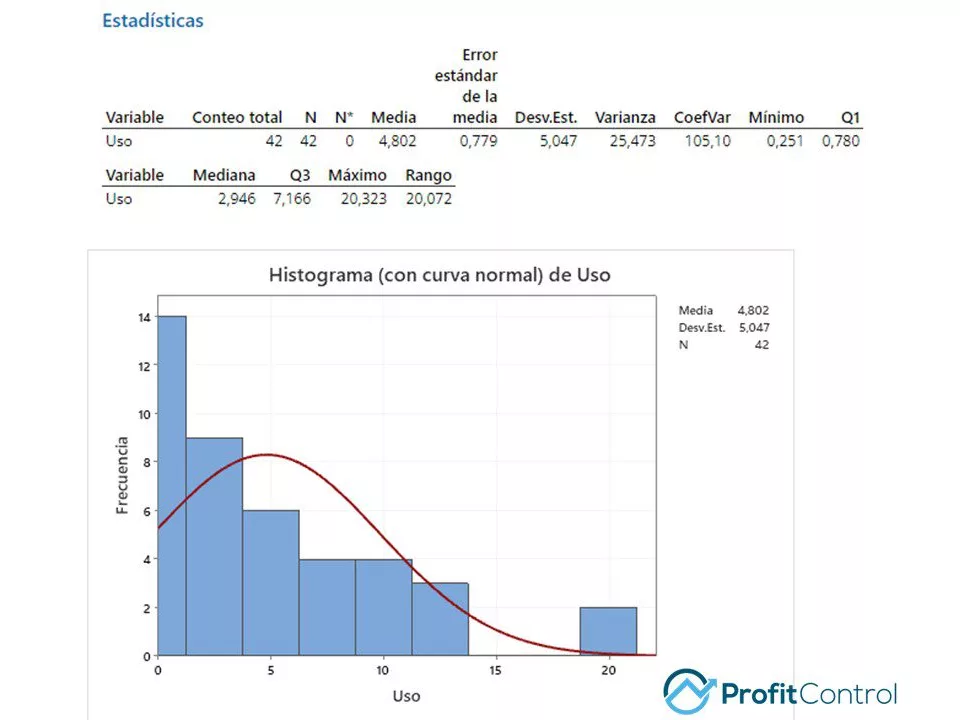
Definitivamente no es normal (pero uno podría esperarlo). Un uso diario mediano de 2,9 gigabytes (GB) y mucha dispersión. Entonces, con 30 días multiplicados por 2,9 GB por día, se espera que el consumo total mensual esté sobre 60… Quizás incluso 70 GB, lo cual está muy en línea con el uso mensual promedio histórico. Hasta ahora, nada revelador. Generemos un gráfico de control para ilustrar el uso en el tiempo desde el principio del último ciclo hasta el día de hoy.
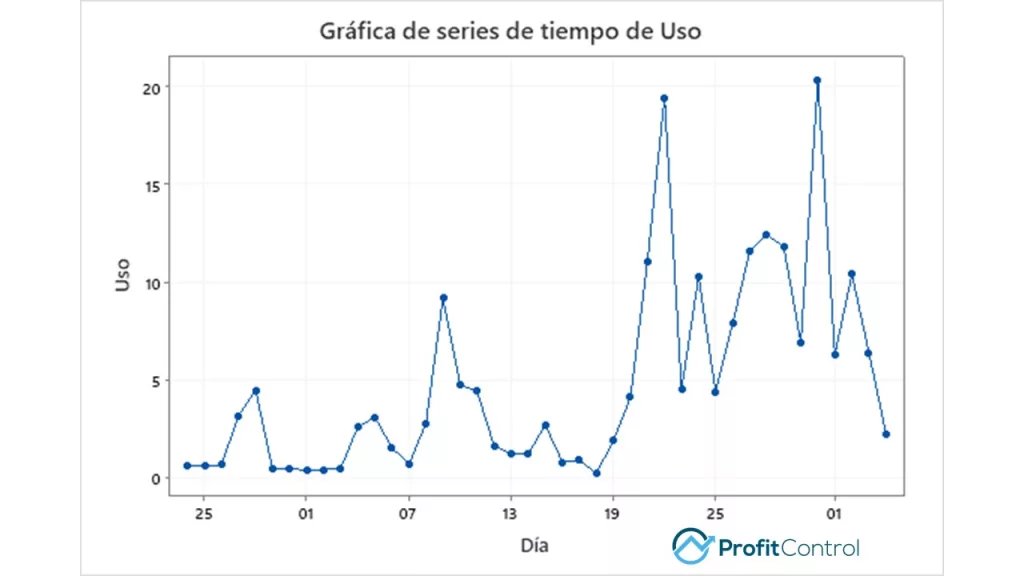
Hmmm… algo no huele bien aquí. El uso se dispara después del 21 de diciembre y se mantiene elevado durante los próximos catorce días. ¿Cuándo regresó nuestra hija a casa durante las vacaciones? ¡Oh, sí! ¡El 21 de diciembre! (Nota: por simplicidad, no entraremos en los valores p asociados con el gráfico de control… No creo que a mi hija le gustaría ese punto en la discusión que surgirá como resultado de este «estudio»). Solo por diversión, generaremos un gráfico de control de estos datos, considerando los valores individuales y tambien las medias móviles.
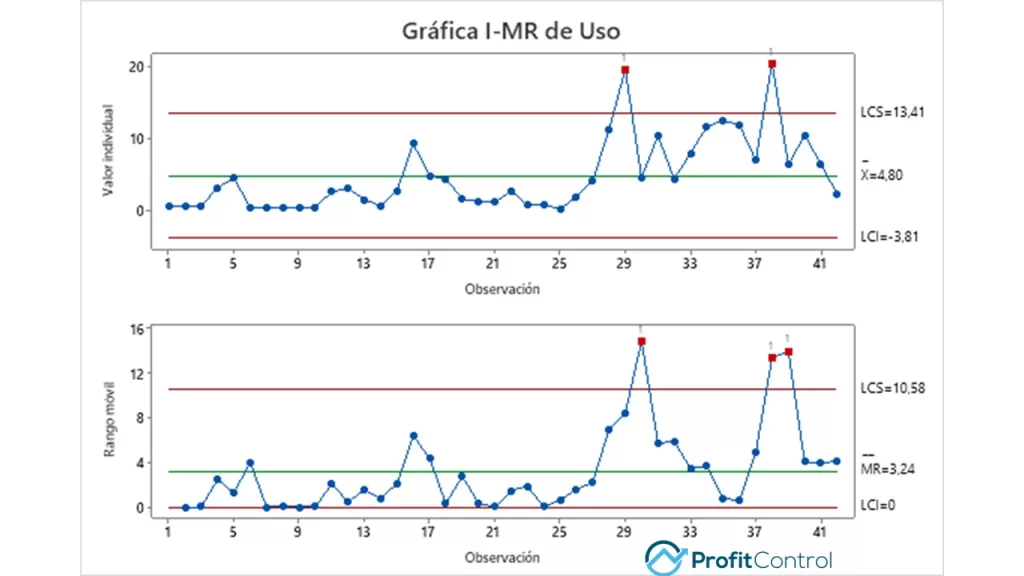
El gráfico de control respalda la suposición de que algo ha «cambiado en el proceso». Hay evidencia de causa especial que ha afectado el proceso. Observación: la hija regresa a casa e interesantemente, el proceso cambia. ¿Correlación? ¿Causa? Podríamos jugar esto hasta el final. Desde que llegó a casa el 21 de diciembre, agregaremos un identificador categórico («Casa – Sí», «Casa – No»), para que podamos agrupar los datos para un análisis posterior.
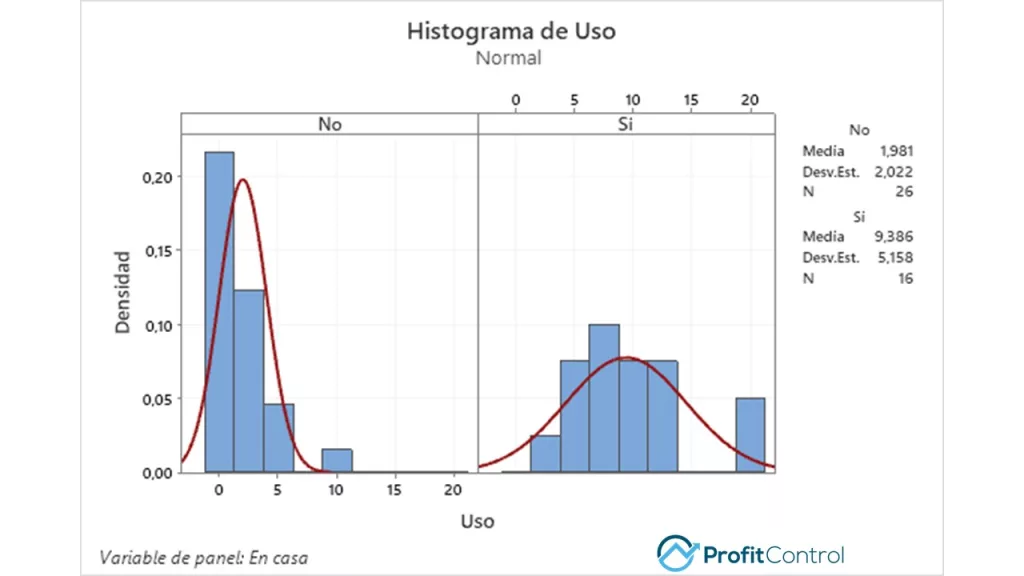
El histograma comparativo y las estadísticas descriptivas anteriores ayudan a ilustrar la diferencia entre «hija en casa» versus «hija fuera de casa». Una cosa que destaca es la diferencia en las medianas de la muestra: 1,9 GB por día cuando la hija no está en casa y 9.4 GB cuando está en casa. Otra observación es la dispersión, hay mucha más variación en el uso diario cuando la hija está en casa. Ahora, para una de mis herramientas favoritas, el diagrama de caja.
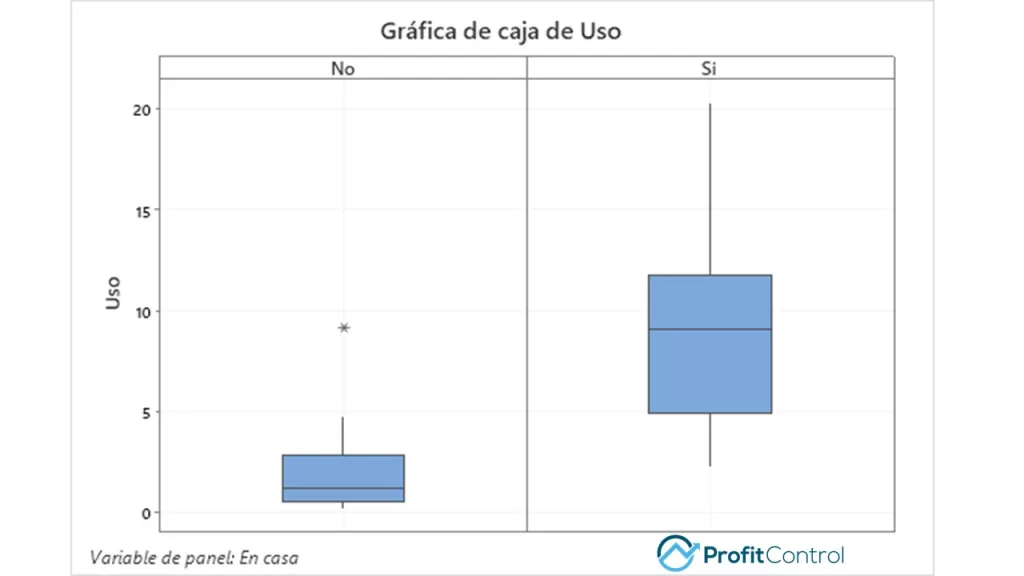
Las diferencias realmente destacan en el gráfico anterior. ¿Notas que tanto la diferencia en la variación (dispersión) como la tendencia central (mediana) se destacan en este gráfico simple pero efectivo? Bueno, tenemos los datos, ¿por qué no ir más allá y realizar un par de pruebas de hipótesis? Primero, probemos si las medias de los dos grupos (hija en casa, hija fuera de casa) difieren. Vemos como claramente, difieren.
Un poco sobre «inocencia» y «culpa»
Hemos aprendido en nuestras clases de Seis Sigma (y estadística) que las pruebas de hipótesis se componen de dos declaraciones… La «hipótesis nula» (inocente hasta que se demuestre lo contrario más allá de una duda razonable) y la «hipótesis alternativa», que es lo contrario de la nula (el rechazo de la suposición de inocencia). La notación «Ho», se utiliza para representar la hipótesis nula y Ha representa la hipótesis alternativa. Cuando rechazamos la suposición de «inocencia» (la Ho), queremos estar seguros de que es la decisión correcta. Queremos que el riesgo de rechazar incorrectamente la hipótesis nula sea bajo (en la mayoría de los casos, menos del 5% de riesgo o 0.05).
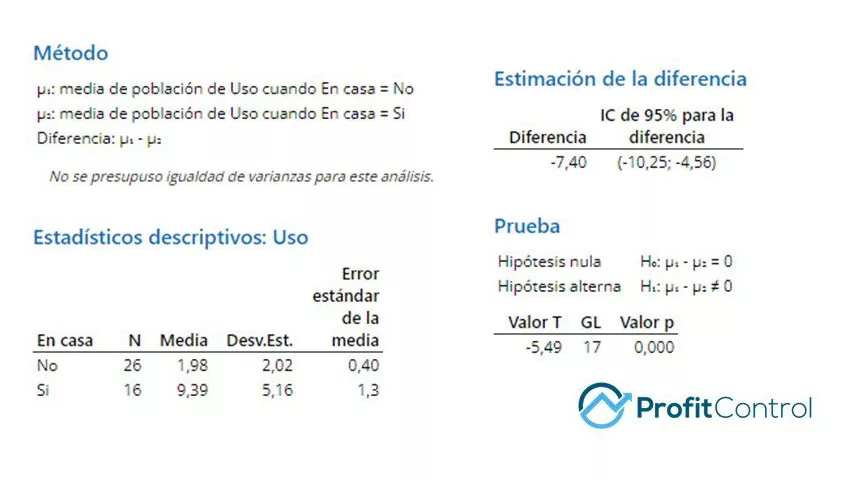
En nuestro ejemplo (anterior), la hipótesis nula (Ho) es que no hay diferencia en la media de los dos grupos (hija en casa, hija fuera de casa). Nuestro riesgo de equivocarnos al rechazar la Ho está representado por el valor p que se muestra en el análisis anterior. Con un valor p de 0.000, prácticamente no hay riesgo de rechazar la hipótesis nula (que afirma que no hay diferencia). Podemos rechazarla con confianza en favor de la hipótesis alternativa y podemos concluir con seguridad que…
Hay una diferencia en el uso diario de GB de cada grupo. El uso es (mucho) mayor cuando la hija está en casa. (Como si esto fuera una sorpresa).
¿De acuerdo? Adelante y hacia arriba. Abordemos el último test… una prueba de comparativa de varianzas, ya que hemos podido comprovar que la variabilidad parece ser diferente. Una vez más, Minitab al rescate… introducimos los datos y, ¡voilà!, interpretamos los resultados.
Lo que es genial acerca de las pruebas de hipótesis es que aunque los «motores» matemáticos difieren de una prueba a otra, el método para la interpretación de los resultados es similar. Recordará del ejemplo anterior que hay dos afirmaciones en su hipótesis:
- Ho (nula): «No hay diferencia en la mediana (uso de Internet) para los dos grupos». «No hay diferencia en la variabilidad para los dos grupos».
- Ha (alternativa): «Hay una diferencia en la mediana (uso de Internet) para los dos grupos». «Hay diferencia en la variabilidad par los dos grupos».
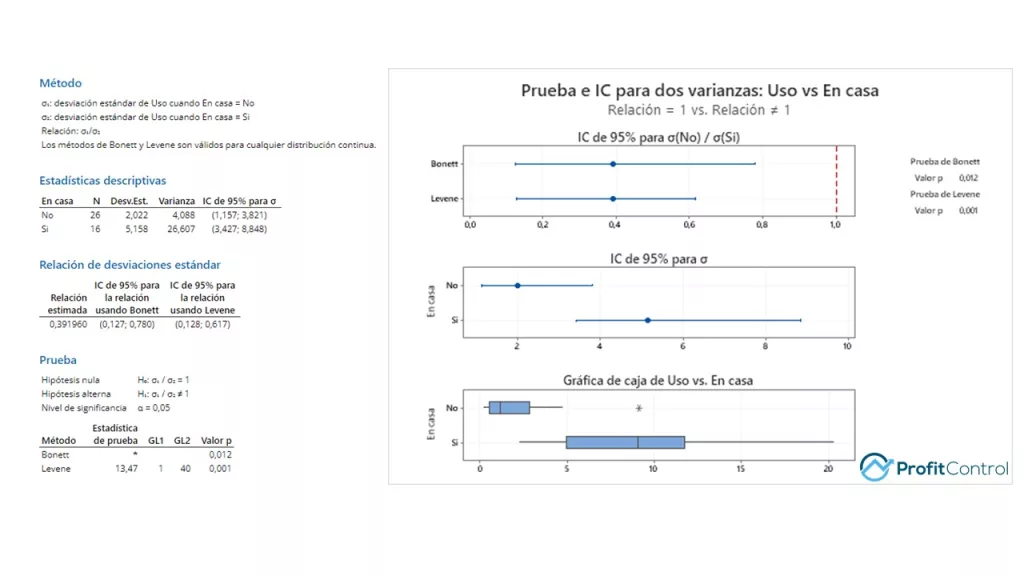
Queremos tener al menos un 95% de confianza de que si rechazamos la nula (Ho) a favor de la alternativa (Ha), estamos en lo correcto al tomar esa decisión. Por lo tanto, nuestro riesgo (representado por el valor p), tiene que ser menor que 0,05. Usted decide… ¿Rechazamos la nula (Ho) a favor de la alternativa (Ha), o no rechazamos la nula? Pista: Mire el valor p en la imagen anterior. En ambos test realizados el resultado es el mismo.
¡CORRECTO! Rechazamos la nula y podemos concluir que hay una diferencia en el uso diario mediano de Internet (GB) cuando la hija está en casa. También existe una diferencia en la variabilidad diaria en el uso de datos.
¿Teniendo dificultades con esta prueba de hipótesis y las reglas para la interpretación? Hay una frase sencilla que resume todo lo que hemos discutido en el ejemplo anterior. Ahora, tienes que decir esto conmigo… dilo bien fuerte… ¿Listo? ¡De acuerdo! Repite después de mí…
Si tenemos un valor p bajo, la H0 puede rechazarse. (O fácil de memorizar en inglés; If the P is low, the ho must go!)
Ahora, si puedes tomarte unos minutos para dejar de reír, terminemos este estudio. Necesito revisar los resultados con mi hija y tomar la acción apropiada para «abordar» el cambio confirmado en el proceso. Cada estudio debe llevar a conclusiones y a una decisión o acción. ¿Qué he aprendido de esto?…
- ¡El uso de Internet aumenta cuando la hija está en casa durante las vacaciones!
- ¡La variación en el uso también aumenta! ¿Las ocasiones en que la hija sale con amigos y participa en el»espíritu» de las vacaciones (y los efectos duraderos de los mismos) pueden resultar en un uso bajo/nulo por ciertos intervalos de tiempo?
- Necesito inmediatamente comprar más capacidad (uso) cuando la hija está en casa (o pagar un «cargo adicional» de $3-4 por GB cuando el plan se excede). Un adicional de 50 GB debería cubrirnos hasta el final del mes, pero tendré que monitorear de cerca.
Aquí está mi observación final y una que fácilmente podría pasarse por alto. ¿Realmente necesito estadísticas para decir lo obvio? Si solo se considerara el gráfico de ejecución y el diagrama de caja, y luego se mirara la situación desde una perspectiva práctica, se podría haber llegado a una conclusión y tomado una decisión.
Las estadísticas descriptivas e inferenciales son herramientas extremadamente poderosas, pero debemos reservar esos métodos y técnicas para decisiones importantes y de alto riesgo cuando la intuición y la observación simple (gráfica) no son suficientes para lograr el nivel de confianza que necesita para tomar una decisión o tomar medidas.
Pero cuando se presenta la oportunidad y se tiene datos para trabajar, intente convertir cada experiencia en una oportunidad para una lección de estadística.
